対称座標法とは

　本記事では三相交流を扱う上で絶大なる力を発揮する数学的ツールである対称座標法というものを導入しよう．詳しい物理的イメージなどは後半でじっくり考えることとして，まずは対称座標法の定義から見ていくことにする．

対称座標法の定義

　対称座標法とは，三相交流の電気量に対して用いられ，下記のような線形変換を用いる計算法のことである．

$$ \begin{pmatrix} V_{0}\\ V_{1}\\ V_{2} \end{pmatrix}=\frac{1}{3} \begin{pmatrix} 1 & 1 & 1\\ 1 & a & a^{2}\\ 1 & a^{2} & a \end{pmatrix} \begin{pmatrix} V_{a}\\ V_{b}\\ V_{c} \end{pmatrix} \tag{1} $$

$$ \begin{pmatrix} V_{a}\\ V_{b}\\ V_{c} \end{pmatrix}= \begin{pmatrix} 1 & 1 & 1\\ 1 & a^{2} & a\\ 1 & a & a^{2} \end{pmatrix} \begin{pmatrix} V_{0}\\ V_{1}\\ V_{2} \end{pmatrix} \tag{2} $$

ここで行列内の定数$a$は

$$a = \frac{-1+j\sqrt{3}}{2} \tag{3}$$

を満たす複素数である．三相交流のa相，b相，c相の電気量である$\left(V_{a}, V_{b}, V_{c}\right)$から0相，1相，2相の電気量である$\left(V_{0}, V_{1}, V_{2}\right)$へと式(1)を用いて変換し，または0相，1相，2相の電気量である$\left(V_{0}, V_{1}, V_{2}\right)$からa相，b相，c相の電気量である$\left(V_{a}, V_{b}, V_{c}\right)$へと式(2)を用いて逆変換することで，三相交流の電気計算を簡略化しようという計算法を対称座標法と呼ぶ．そして0相を零相，1相を正相，2相を逆相と呼ぶ．

　上記の定義を見て，早速理解を諦める読者が続出してしまいそうなので予め断っておくが，見た目よりもその物理的イメージやその計算ははるかに単純である．これからそのイメージを一つずつ説明していくことにしよう．

対称座標法のイメージ（１）～正相成分～

　対称座標法というのはa相・b相・c相の電気量を零相・正相・逆相の電気量に変換したり，また逆方向に変換しなおしたり，といった演算を基本とする計算法であったから，何よりも先にまず，零相・正相・逆相の物理的描像を理解するところから出発するべきだろう．

　最初に正相成分のイメージを説明しよう．交流理論において正相成分が一番基本的な電圧成分（電流成分も）となるからである．正相成分のみが存在している状況は，a相・b相・c相においてどのように見えるのか，実際に計算してみる．正相成分のみ$0$ではないから，

$$ \begin{pmatrix} V_{0}\\ V_{1}\\ V_{2} \end{pmatrix}= \begin{pmatrix} 0\\ V_{1}\\ 0 \end{pmatrix} \tag{4} $$

これをa相・b相・c相の領域に逆変換するべく，式(2)を用いると

$$ \begin{pmatrix} V_{a}\\ V_{b}\\ V_{c} \end{pmatrix}= \begin{pmatrix} 1 & 1 & 1\\ 1 & a^{2} & a\\ 1 & a & a^{2} \end{pmatrix} \begin{pmatrix} 0\\ V_{1}\\ 0 \end{pmatrix}= V_{1}\begin{pmatrix} 1\\ a^{2}\\ a \end{pmatrix} \tag{5} $$

という風に$\left(V_{a}, V_{b}, V_{c}\right)$を求めることができる．これが，正相成分のみを持つ場合のa相・b相・c相の電圧（フェザー表示）となるのである．ここで，$a$は式(3)で与えられる複素数であり，

$$\left|{a}\right| = 1, arg\left({a}\right)=120^{\circ} \tag{6}$$

を満たすから，$1, a, a^{2}$はすべて大きさが$1$であり，偏角が$0^{\circ}, 120^{\circ}, 240^{\circ}$となるため，$\left(V_{a}, V_{b}, V_{c}\right)$は次の図1のように描くことができる．

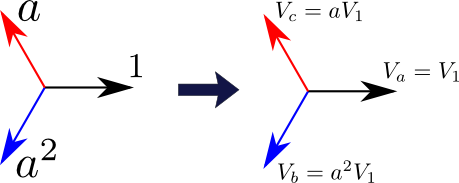
図1.$\left(1,a,a^{2}\right)$のフェザー表示（左）と正相成分のみの場合の$\left(V_{a}, V_{b}, V_{c}\right)$のフェザー表示（右）

　図1の左側は$1, a, a^{2}$を表し，右側はそれに対応して$\left(V_{a}, V_{b}, V_{c}\right)$を表している．これによると，$V_{a}$→$V_{b}$→$V_{c}$の順で時計回りに$120^{\circ}$ずつ回転しているような図になっている．これが正相成分の電気的なイメージである．これはフェザー表示の話なので，実際の波形も含めてまとめ直すと下記の図2のように書き表される．

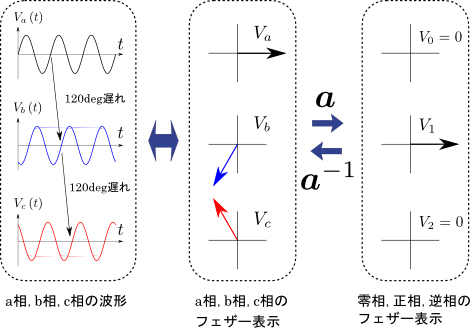
図2.正相成分のみの場合のa相・b相・c相の波形

　フェザー表示において$V_{a}$→$V_{b}$→$V_{c}$の順で時計回りに$120^{\circ}$ずつ回転していたので，実際の波形を見ると，a相→b相→c相の順で$120^{\circ}$ずつ位相が遅れることになる．つまり，理想的な三相交流電圧を対称座標法で表すと，正相成分のみが値を持つことになることがわかる．ここで，図2の真ん中と右側を結ぶ行列$\boldsymbol{a}$と逆行列$\boldsymbol{a}^{-1}$は，次の行列のことを指す．

$$ \boldsymbol{a}=\frac{1}{3} \begin{pmatrix} 1 & 1 & 1\\ 1 & a & a^{2}\\ 1 & a^{2} & a \end{pmatrix} \tag{7} $$

$$ \boldsymbol{a}^{-1}= \begin{pmatrix} 1 & 1 & 1\\ 1 & a^{2} & a\\ 1 & a & a^{2} \end{pmatrix} \tag{8} $$

単純に$\boldsymbol{a}$や$\boldsymbol{a}^{-1}$は，式(1)や式(2)の座標変換・逆変換の行列を抜き出したものである．次に逆相成分の電気的イメージも調べてみることにしよう．

対称座標法のイメージ（２）～逆相成分～

　逆相成分についても，上記の正相成分のときと同じ計算を適用する．つまり次の式(9)に示すように，逆相成分のみ$0$ではない$\left(V_{0}, V_{1}, V_{2}\right)$を想定する．

$$ \begin{pmatrix} V_{0}\\ V_{1}\\ V_{2} \end{pmatrix}= \begin{pmatrix} 0\\ 0\\ V_{2} \end{pmatrix} \tag{9} $$

これをa相・b相・c相の領域に逆変換するべく，式(2)を用いると

$$ \begin{pmatrix} V_{a}\\ V_{b}\\ V_{c} \end{pmatrix}= \begin{pmatrix} 1 & 1 & 1\\ 1 & a^{2} & a\\ 1 & a & a^{2} \end{pmatrix} \begin{pmatrix} 0\\ 0\\ V_{2} \end{pmatrix}= V_{2}\begin{pmatrix} 1\\ a\\ a^{2} \end{pmatrix} \tag{10} $$

という風に$\left(V_{a}, V_{b}, V_{c}\right)$を求めることができる．これが，逆相成分のみを持つ場合のa相・b相・c相の電圧（フェザー表示）となる．ここで，図1で示したように$1, a, a^{2}$はすべて大きさが$1$であり，偏角が$0^{\circ}, 120^{\circ}, 240^{\circ}$となるため，$\left(V_{a}, V_{b}, V_{c}\right)$は次の図3のように描くことができる．

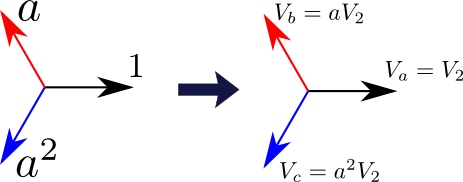
図1.$\left(1,a,a^{2}\right)$のフェザー表示（左）と逆相成分のみの場合の$\left(V_{a}, V_{b}, V_{c}\right)$のフェザー表示（右）

　これによると，$V_{a}$→$V_{b}$→$V_{c}$の順で反時計回りに$120^{\circ}$ずつ回転しているような図になっている．これが逆相成分の電気的なイメージであり，位相関係が正相のときとは逆向きになっていることがわかるだろう．これも実際の波形においては下記の図4のように書き表される．

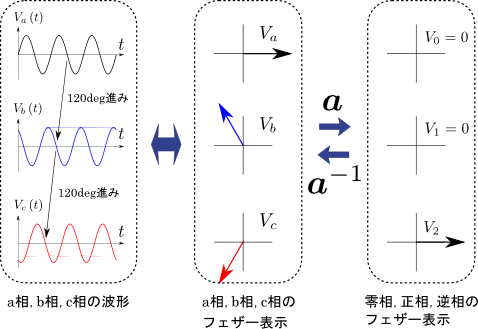
図4.逆相成分のみの場合のa相・b相・c相の波形

　正相のときとは逆に，逆相成分のみの場合においては，a相→b相→c相の順に位相が$120^{\circ}$ずつ進んでいる．最後に零相成分のイメージも考察しよう．

対称座標法のイメージ（３）～零相成分～

　零相成分についても同様にして，下記のように零相成分のみ$0$ではない$\left(V_{0}, V_{1}, V_{2}\right)$を想定して話を進める．

$$ \begin{pmatrix} V_{0}\\ V_{1}\\ V_{2} \end{pmatrix}= \begin{pmatrix} V_{0}\\ 0\\ 0 \end{pmatrix} \tag{11} $$

これをa相・b相・c相の領域に逆変換するべく，式(2)を用いると

$$ \begin{pmatrix} V_{a}\\ V_{b}\\ V_{c} \end{pmatrix}= \begin{pmatrix} 1 & 1 & 1\\ 1 & a^{2} & a\\ 1 & a & a^{2} \end{pmatrix} \begin{pmatrix} V_{0}\\ 0\\ 0 \end{pmatrix}= V_{0}\begin{pmatrix} 1\\ 1\\ 1 \end{pmatrix} \tag{12} $$

という風に$\left(V_{a}, V_{b}, V_{c}\right)$を求めることができる．零相成分のみの場合はa相・b相・c相の電圧（フェザー表示）がすべて等しいという結果になる．つまり零相成分のみの場合のa相・b相・c相の波形は下記の図5のようになる．

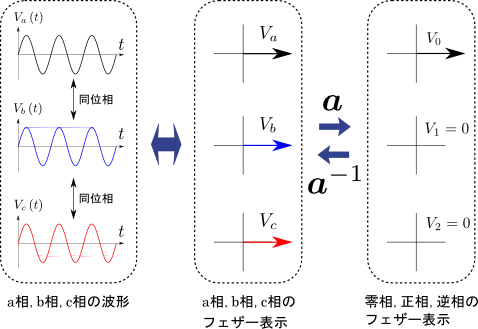
図5.零相成分のみの場合のa相・b相・c相の波形

　三相ともに同じ位相・振幅となっているとき，零相成分のみとなっており，これが零相成分の電気的イメージとなっている．正相・逆相・零相のそれぞれについて物理的描像を説明したので，最後に対称座標法全体のイメージを説明したい．

対称座標法全体のイメージ

　ここまでで，零相・正相・逆相がどのような物理的イメージを持つのか，電圧を題材にして説明してきた．ここでも電圧を題材に，零相電圧を$V_{0}$，正相電圧を$V_{1}$，逆相電圧を$V_{2}$とおいて話を進める．対称座標法というのは，a相・b相・c相の電圧成分$\left(V_{a}, V_{b}, V_{c} \right)$と零相・正相・逆相の電圧成分$\left(V_{0}, V_{1}, V_{2} \right)$との間を$3\times{3}$の複素行列で線形変換・逆変換することを用いた計算法のことを指す．

図6.対称座標法の変換イメージ

　ここで，$\left(V_{a}, V_{b}, V_{c} \right)$も$\left(V_{0}, V_{1}, V_{2} \right)$も複素量であることに注意が必要である．つまりこれらは実際の実数的な電気量ではなく，一般にはフェザー表示について適用される計算法である．もちろん，

$$ \begin{pmatrix} V_{0}\left({t}\right)\\ V_{1}\left({t}\right)\\ V_{2}\left({t}\right) \end{pmatrix}=\boldsymbol{a} \begin{pmatrix} V_{a}\left({t}\right)\\ V_{b}\left({t}\right)\\ V_{c}\left({t}\right) \end{pmatrix} \tag{13} $$

$$ \begin{pmatrix} V_{a}\left({t}\right)\\ V_{b}\left({t}\right)\\ V_{c}\left({t}\right) \end{pmatrix}= \boldsymbol{a}^{-1} \begin{pmatrix} V_{0}\left({t}\right)\\ V_{1}\left({t}\right)\\ V_{2}\left({t}\right) \end{pmatrix} \tag{14} $$

というように，時間変化する実際の波形を$\left(V_{a}, V_{b}, V_{c} \right)$に当てはめて考えることもできるわけだが，この計算が意味を持つのは，

$$ \begin{pmatrix} V_{a}\left({t}\right)\\ V_{b}\left({t}\right)\\ V_{c}\left({t}\right) \end{pmatrix}= \begin{pmatrix} V_{a0}\left({t}\right)e^{j\omega{t}+\phi_{a}\left({t}\right)}\\ V_{b0}\left({t}\right)e^{j\omega{t}+\phi_{b}\left({t}\right)}\\ V_{c0}\left({t}\right)e^{j\omega{t}+\phi_{c}\left({t}\right)} \end{pmatrix} $$

などのように$V_{a}\left({t}\right), V_{b}\left({t}\right), V_{c}\left({t}\right)$が複素量で表されているときである．過渡現象を深く扱うことがなく，純粋に単一周波数の定常状態を解析するだけであれば，単純に「$\left(V_{a}, V_{b}, V_{c} \right)$も$\left(V_{0}, V_{1}, V_{2} \right)$もフェザー表示」と割り切ってもらっても差し支えは無いだろう．

　また，今回は電圧を題材にしたが，もちろん電流や皮相電力などあらゆる三相電気量についてこの変換を当てはめることができる．次の記事においては電流なども変換しつつ，この計算方法が実際の系においてどのように役立つのか，具体的に説明していきたい．