直流機の起電力

 

　続いて今度は直流機（直流電動機でも直流発電機でも全く同じ議論が成り立つ）の起電力の大きさについて考えてみる．これもトルクを計算したときと同様，もっとも単純な例である下記の図1（整流子型直流機）を例にとって計算していくことにしよう．

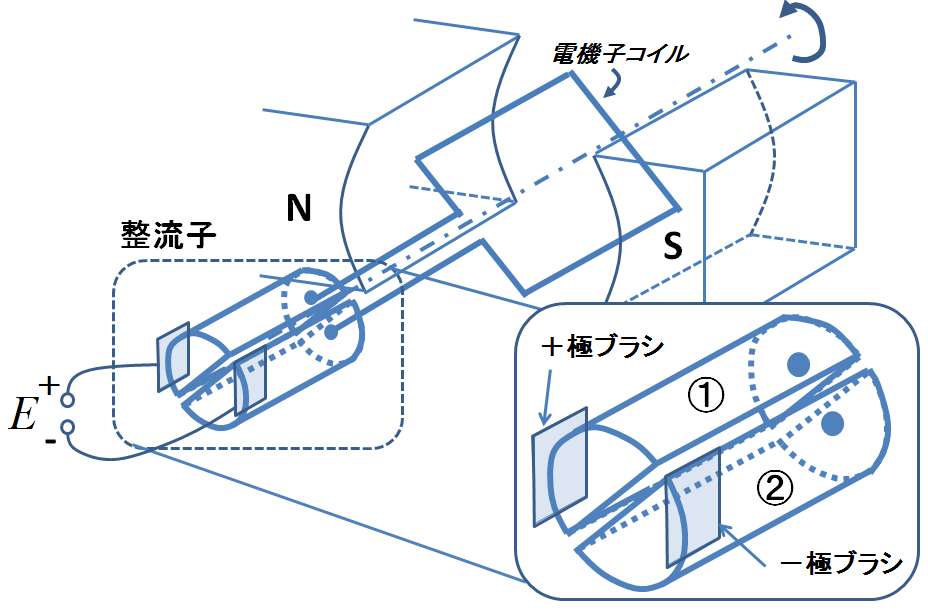
図1.整流子型直流機

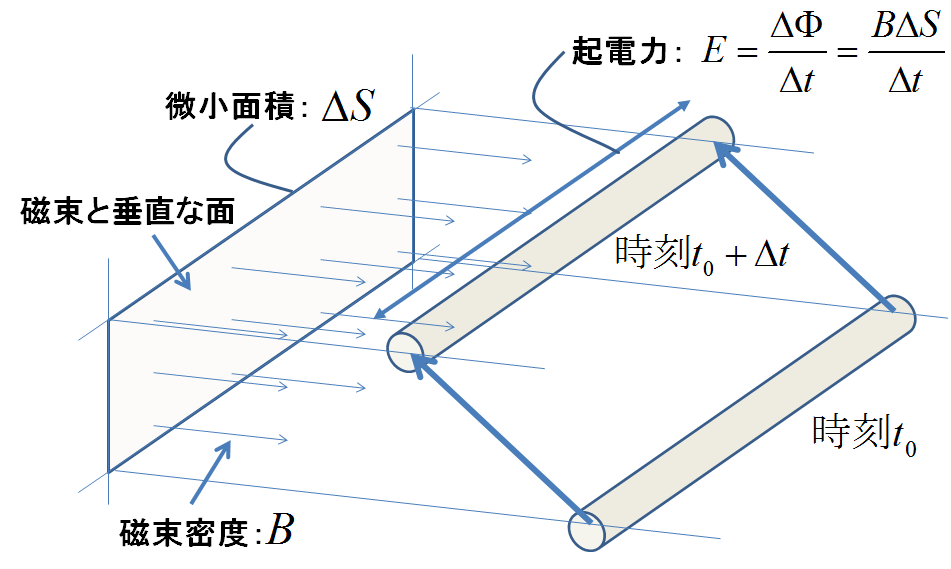
図2.ファラデーの法則


 

　図1の直流機が回転しているときの誘導起電力がどのように決まるのか，その物理的イメージを理解することが今回のゴールだが，そのために是が非でも知っておくべき物理法則として，ファラデーの法則がある．図2には，直流機の誘導起電力を求める上で都合の良いように表現をアレンジしたファラデーの法則を表している．ここは非常に重要なので，ここでしっかり明記しておきたい．

磁場中で導線に生じる起電力の大きさ\(E\)は，

その導線が微小時間\(\Delta t\)の間に横切った磁束を\(\Delta\Phi\)としたとき，

$$E=\frac{\Delta\Phi}{\Delta t}\tag{a}$$

と表わされる

　つまり，導体に生じる起電力の大きさは，単位時間に横切る磁束の量により決まるのである．分かりやすく言うと，磁束を稲だとして導体を刃物だとすると，稲穂を刈り取る能率が起電力の大きさとなる．そのイメージを持ってもう一度図1を眺めてみると，稲穂を刈り取っているのは回転軸に平行な2本の導体だけで，回転軸と垂直な残りの導体は稲を全く刈り取っておらず，起電力には寄与しないことが直感的に理解できるだろう．起電力に寄与する導体部分と寄与しない導体部分を示したものが次の図3になる．

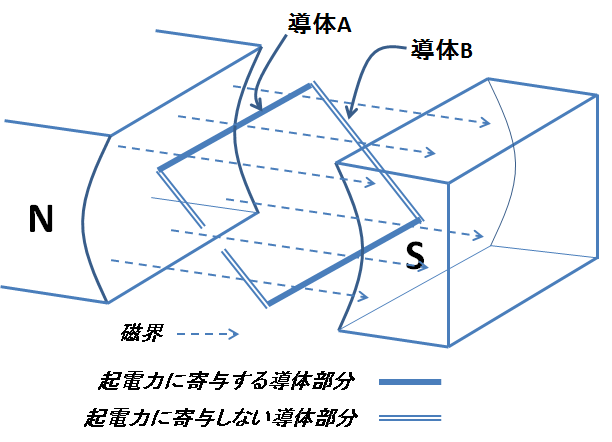
図3.起電力が生じる導線部分

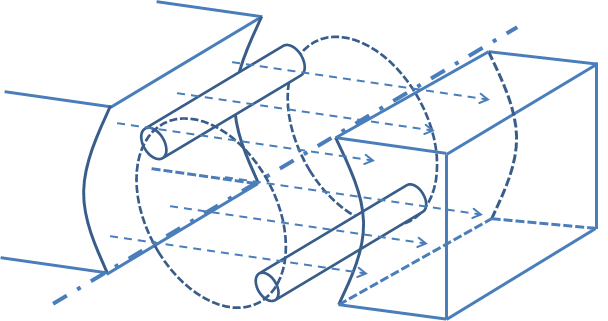
図4.起電力計算のための2本の導線


 

　図3を見ると，導体1周分の起電力を求めたければ，純粋に図4に示すような導体2本を抜き出してやり，この2本の導体に発生する起電力の和をとってやればよいことがわかる．

　それではこれから図4の導体に発生する起電力を，上記の図2で示したファラデーの法則を用いて求めていこう．計算を始める下準備として，下の図5のように，起電力を計算するために必要なパラメータを定義しておく．

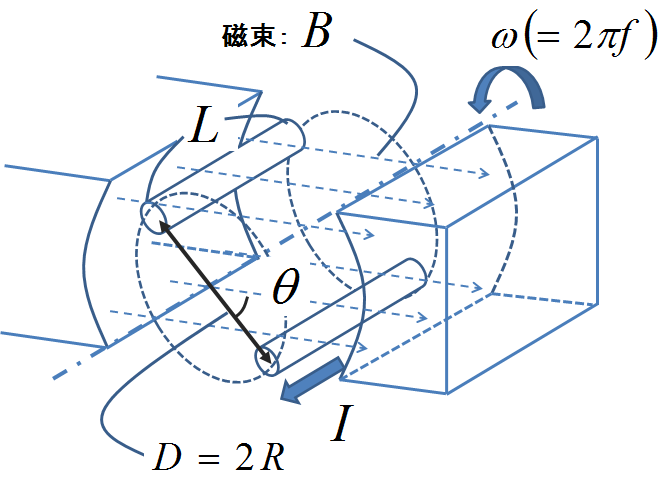
図5.起電力計算のためのパラメータ

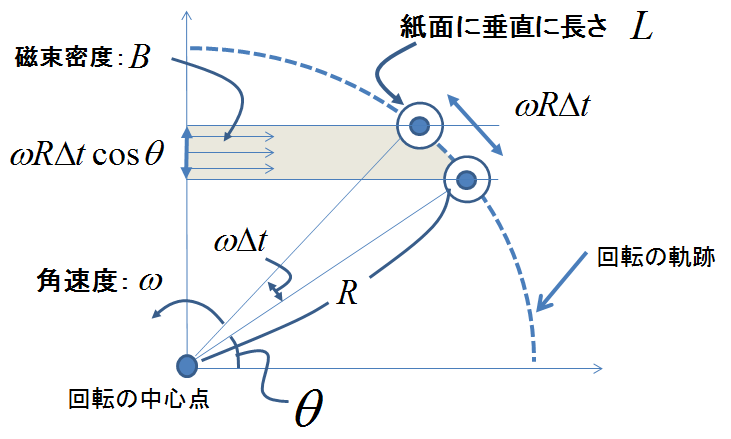
図6.導体1本の起電力計算


 

　図2と図5から，図5の導体1本の起電力を求めるためには図6のような絵を描いてみればよいことがわかる．導体が微小時間\(\Delta t\)の間に刈り取る磁束\(\Delta\Phi\)は，同図の灰色で示した帯に収まっている磁束に等しいので，それを求めればこの問題は解けたも同然である．まず角速度が\(\omega\)で中心からの距離が\(R\)なので，微小時間\(\Delta t\)の間に導線が進んむ距離は\(\omega R\Delta t\)となる．これの縦軸方向成分である\(\omega R\Delta t \cos\theta\)が灰色領域の高さに相当する．一方この灰色領域の紙面に対する奥行は\(L\)で，かつ磁束密度は\(B\)なので，灰色領域に収まっている磁束\(\Delta\Phi\)は，

$$\Delta\Phi=\omega BLR\Delta t\:\cos\theta \tag{1}$$

　と求まるだろう．ここで上の方で説明したファラデーの法則の式（a）を思い出すと，上記の式（1）を微小時間で割れば1本当たりの起電力が導かれる．今回の図1のケースは導体が2本なので，結局起電力の大きさ\(E\)は次の式（2）のように求められる．

$$E=\frac{2\Delta\Phi}{\Delta t}=2\omega BLR\:\cos\theta \tag{2}$$

　これで図1に示したもっとも単純な直流機の起電力が計算できたと言いたいところなのだが，まだここで一つ忘れていることがある．それは，この式が成り立つの範囲は，\(0\leq \theta \leq \frac{\pi }{2}\) であるということである．トルクの計算のときもまったく同じ議論をしたが，改めてどういうことか，まずはこの式（2）の起電力を回転角度\(\theta\)を横軸にとって何周期分かプロットして図7をご覧いただきたい．

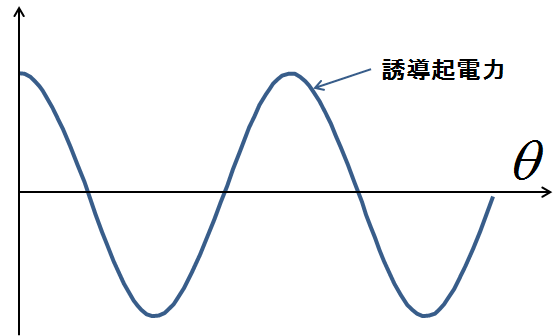
図7.整流子を考慮に入れないときの起電力

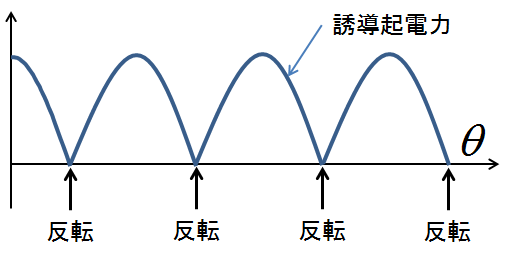
図8.整流子を考慮に入れた起電力


 

　まず図7を見ると，起電力が半回転するごとに正負逆転しており，一方向に定まった起電力ではない．これでは直流ではなくむしろ交流である．そこで直流機では，整流子を使って半周回転（2極の場合）ごとに接続の極性を反転させ，常に一つの方向に起電力が発生させるように工夫していたのだった．そのことを思い出せば，図7で示した起電力のグラフは，図8のように変更されることがわかる．つまり，整流子の効果によって図7の交流の起電力を常に一定の方向に（ここでは正の符号に）折り返したようなグラフが，実際の直流機で発揮される起電力のグラフになると言える．

　すなわち，式（2）の起電力の結果は整流子の効果を考慮すると，下記の（3）の形に書き換えられるだろう．

$$E=2\omega BLR\:\left | \cos\theta \right | \tag{3}$$

　これにて図1で示したもっとも単純な直流機における誘導起電力を計算することができた．

　しかしこの結果は回転角度\(\theta\)ににおいて導体に発生する瞬間的な起電力である．一方で我々が必要としている起電力は，この時間平均だろう．つまり，下記の図9における\(\overline{E}\)を計算する必要がある．

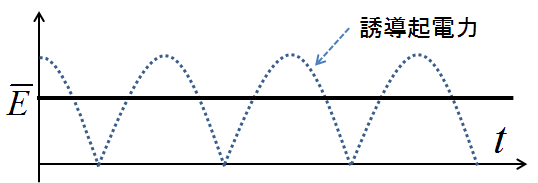
図9.瞬間的な起電力と平均起電力

 

　ここで，横軸は\(\theta\)から時間\(t\)に変更した．定速で回転している分にはこの置き換えにより横方向のスケールが変わるだけでである．求めたいのは時間平均だが，計算しやすいのは\(\theta\)上での平均であろう．定速で回転していれば両者の平均は同じなので，今回は\(\theta\)上で式（3）の平均を計算してみる．

$$\begin{eqnarray*} \overline{E}=\frac{1}{\frac{\pi}{2}}\int_{0}^{\frac{\pi}{2}}Ed\theta &=&\frac{2}{\pi}\int_{0}^{\frac{\pi}{2}}2\omega BLR\left | \cos\theta \right |d\theta\\ &=&\frac{2}{\pi}\int_{0}^{\frac{\pi}{2}}2\omega BLR\cos\theta d\theta\\ &=&\frac{4\omega BLR}{\pi} \tag{4} \end{eqnarray*}$$

　回転角度\(\theta\)の依存性が消えて，定数になった．このように起電力を時間について平均化した定数として扱っていい理由としては，寄生インダクタなどによる急峻な電圧変動を平滑化するような電気的状況も挙げることができるが，何よりも重要なイメージとしては，以下の図10のような状況があるだろう．

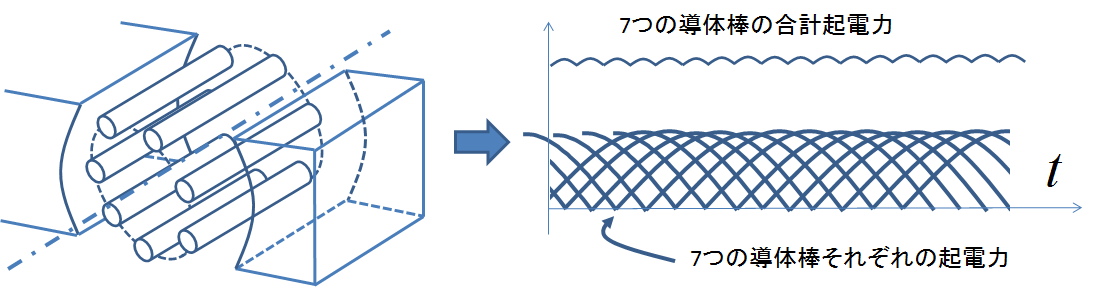
図10.分布的に導体数が増えた直流機の誘導起電力

 

　このように分布的に導体の本数が増えた場合は，少しずつ位相のずれた起電力を足し合わせることで全体として起電力変動が少ない直流機を構成することができる．この場合は，電流を流す導体1本当たり，式（4）で示した値の半分の起電力が寄与していると言える．（式（4）は導体2本分の結果）

　ここで，式（4）は磁束密度\(B\)を用いて表しているが，この磁束密度\(B\)は回転位置\(\theta\)の関数であり，本来\(B(\theta)\)と表されるべきものであろう．そしてこの関数\(B(\theta)\)の詳細がわからないと，式（4）の値も分からないということになり大変不便である．よって，トルクの計算のときにも同じ議論をしたが，一般的には磁極1つ当たりの磁束\(\Phi\)で起電力を表すということをする．式（4）の積分を，磁束密度\(B(\theta)\)として計算しなおすことにより磁束\(\Phi\)で表してみよう．

$$\begin{eqnarray*} \overline{E}=\frac{1}{\frac{\pi}{2}}\int_{0}^{\frac{\pi}{2}}Ed\theta &=&\frac{2}{\pi}\int_{0}^{\frac{\pi}{2}}2\omega B(\theta)LR\left | \cos\theta \right |d\theta\\ &=&\frac{4\omega}{\pi}\int_{0}^{\frac{\pi}{2}}B(\theta)LR\cos\theta d\theta\\ &=&\frac{4\omega}{\pi}\cdot\frac{\Phi}{2}\\ &=&\frac{2\omega\Phi}{\pi} \tag{5} \end{eqnarray*}$$

　これで磁束密度\(B\)が回転角度\(\theta\)に依存していようとも，1極当たりの磁束\(\Phi\)で起電力を表すことができた．これが，図1に記したもっとも単純な直流機の起電力の最終的な答えである．上記の2行目から3行目への積分は，1/4周分の導体の軌跡で作られる面上における磁束密度の面積分となるので，積分部分の値は，1極当たりの磁束\(\Phi\)の丁度半分になる．これにより，磁束密度分布によらず，1極当たりの磁束\(\Phi\)で起電力を表すことができた．図1は導体が2本あったので，導体1本当たりの起電力\(\overline{E_1}\)は下記のように表すことができる．

$$\overline{E_1}=\frac{\omega\Phi}{\pi} \tag{6}$$

 

　ここまでで直流機の誘導起電力の基本的説明は終了である．トルク計算とかなり共通のイメージが湧いたのではないだろうか．実際にはトルクの解析と同様，並列回路数や総導体数，極数などにより，上記に示した起電力の結果は勿論変化する．ただし，使う物理法則と解析のアプローチは常に上記の説明と共通である．

 

 

 

この項の内容に関する，より詳細で完全な解説は，【徹底解説　電動機・発電機の理論】のP.80～P.94にて展開されています．
是非ご参照を!!

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス