短絡比と電圧変動率

 

　ここでは短絡比と電圧変動率の説明をする．この二つの指標の物理的意味を考察する前に，まずは下記の図1を見つつ両者の定義をおさらいしてみよう．

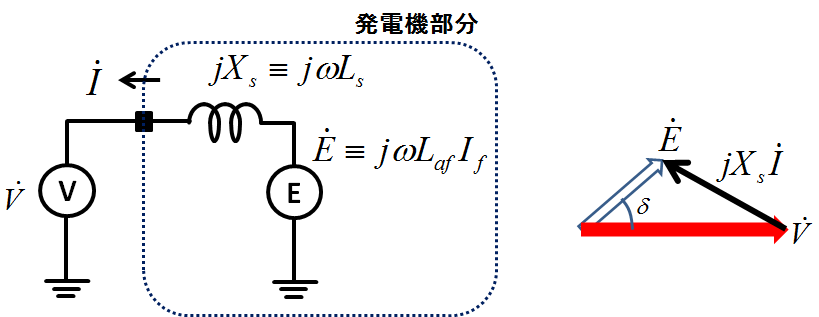
図1.同期発電機の等価回路とベクトル図

 

　この図1は同期発電機の等価回路とそのベクトル図を表している．短絡比というのは平たく言えば同期インピーダンスの低さを表す指標である．例えば図1中の同期リアクタンス\(X_{s}\)が小さくなれば短絡比は大きくなる．具体的には定格端子電圧(ベクトル図上の電圧なので相電圧)を\(V_{n}\)，定格電流を\(I_{n}\)とすると短絡比\(K_{s}\)は以下のようになる．

$$ K_{s}=\frac{V_{n}}{I_{n}X_{s}} \tag{1} $$

 

また電圧変動率というのは，負荷電流を変化させたときに端子電圧がどれだけ変動するかを表した指標で，短絡比が大きい方が同期インピーダンスが低いので電圧変動率も小さい．具体的には，定格運転しているときの端子電圧\(\left|\dot{V}\right|\)と，そのままの励磁電流で無負荷にしたときの端子電圧\(V_{0}\)を用いると電圧変動率\(\epsilon\)[%]は，

$$ \epsilon=\frac{V_{0}-\left|\dot{V}\right|}{\left|\dot{V}\right|}\times{100} \tag{2} $$

と表される．図1を見れば直感的にもわかるが，負荷電流\(\dot{I}\)が小さくなれば端子電圧\(\left|\dot{V}\right|\)は起電力\(\left|\dot{E}\right|\)に近づいていく．つまり式（2）は次の式（3）のようにも書ける．

$$ \epsilon=\frac{\left|\dot{E}\right|-\left|\dot{V}\right|}{\left|\dot{V}\right|}\times{100} \tag{3} $$

　要するに定格運転時の端子電圧と起電力が近ければ電圧変動率が小さくなる．そしてそのときは\(I_{n}X_{s}\)が小さくなるので式（1）から短絡比が大きくなっている．この辺りのイメージを，具体的なベクトル図で確かめてみよう．次の図2を見ていただきたい．

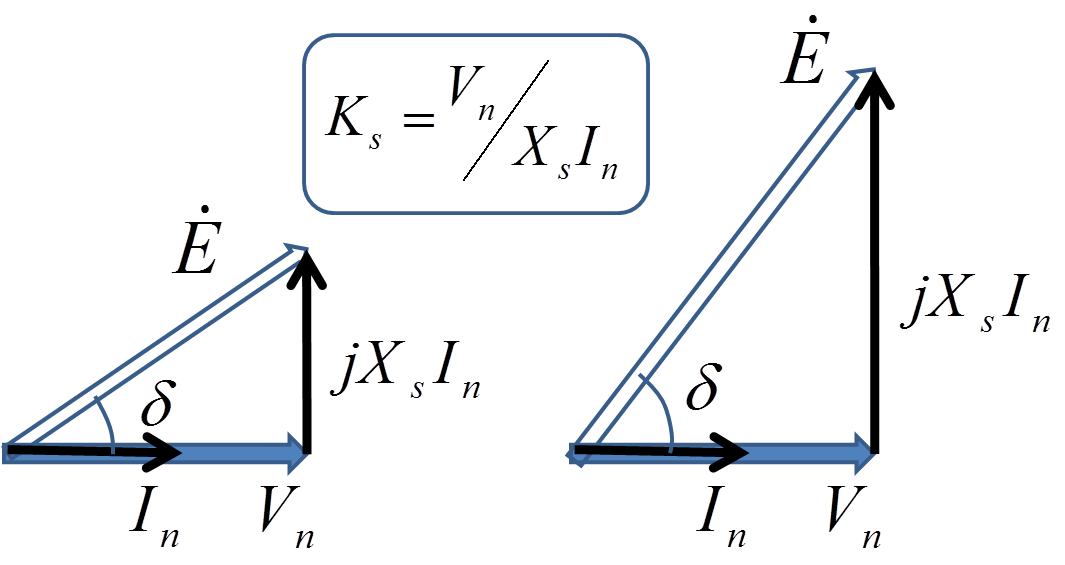
図2.短絡比と電圧変動率（力率角\(0\)）

 

　この図2は，力率が\(1\)（力率角が\(0\)）のときの２つのベクトル図を示している．左側は\(X_{s}I_{n}\)が小さいので式（1）より短絡比\(K_{s}\)は大きく，\(\left|\dot{E}\right|\)が\(V_{n}\)に近いため電圧変動率\(\epsilon\)は小さい．一方で右側は\(X_{s}I_{n}\)が大きいので式（1）より短絡比\(K_{s}\)は小さく，\(\left|\dot{E}\right|\)が\(V_{n}\)から遠いため電圧変動率\(\epsilon\)は大きくなる．要するに電流\(I_{n}\)によって電圧が大きく変化するか否かはベクトル図上で\(jX_{s}I_{n}\)の長さに注目してやればよいのである．

　それでは実際に短絡比を測定するためにはどのような試験をすればよいのか説明していきたい．短絡比を測るには以下の図3に示すような２つの試験を行う必要がある．

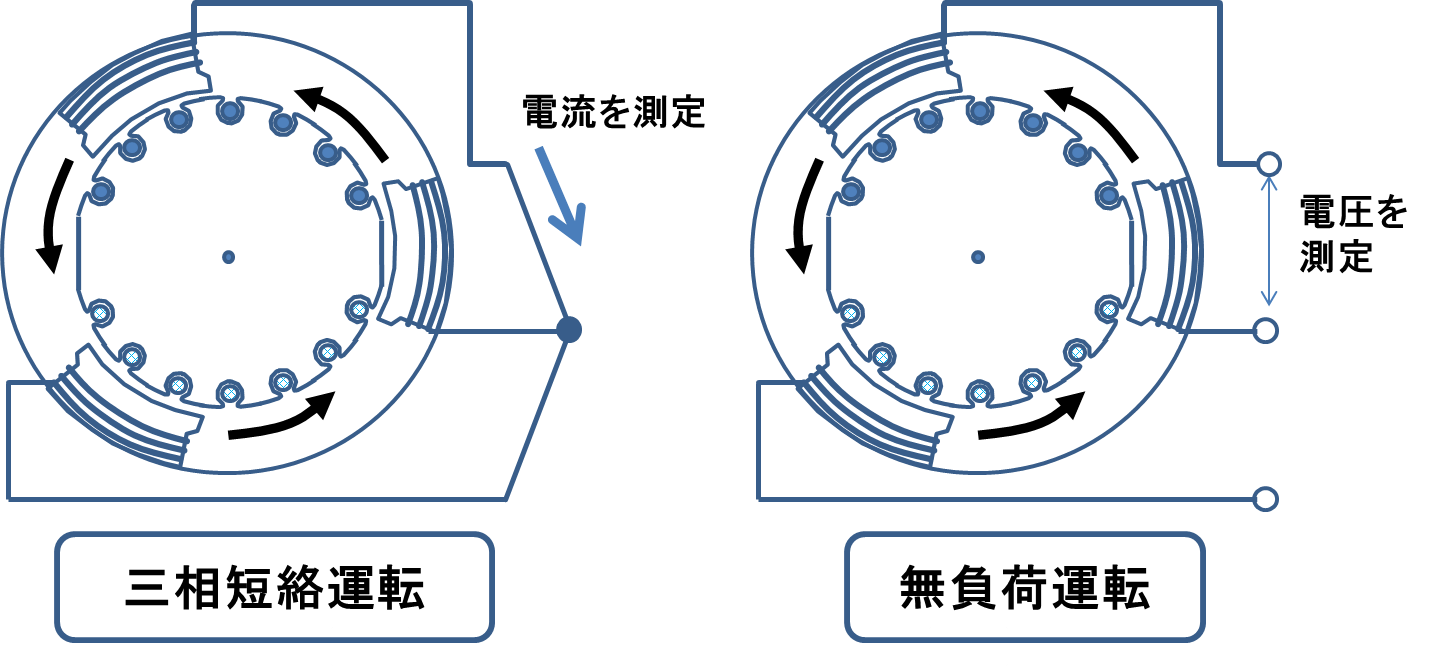
図3.三相短絡試験（左）と無負荷試験（右）

 

　図3の左側は三相短絡試験，右側は無負荷試験を表している．左の三相短絡試験は三相を短絡させ，励磁電流\(I_{f}\)を変化させながら短絡電流を測定するという試験であり，右の無負荷試験は逆に三相をオープン（無負荷）にし，同じく励磁電流\(I_{f}\)を変化させつつ端子電圧を測定するという試験である．その結果は下の図4のようになる．

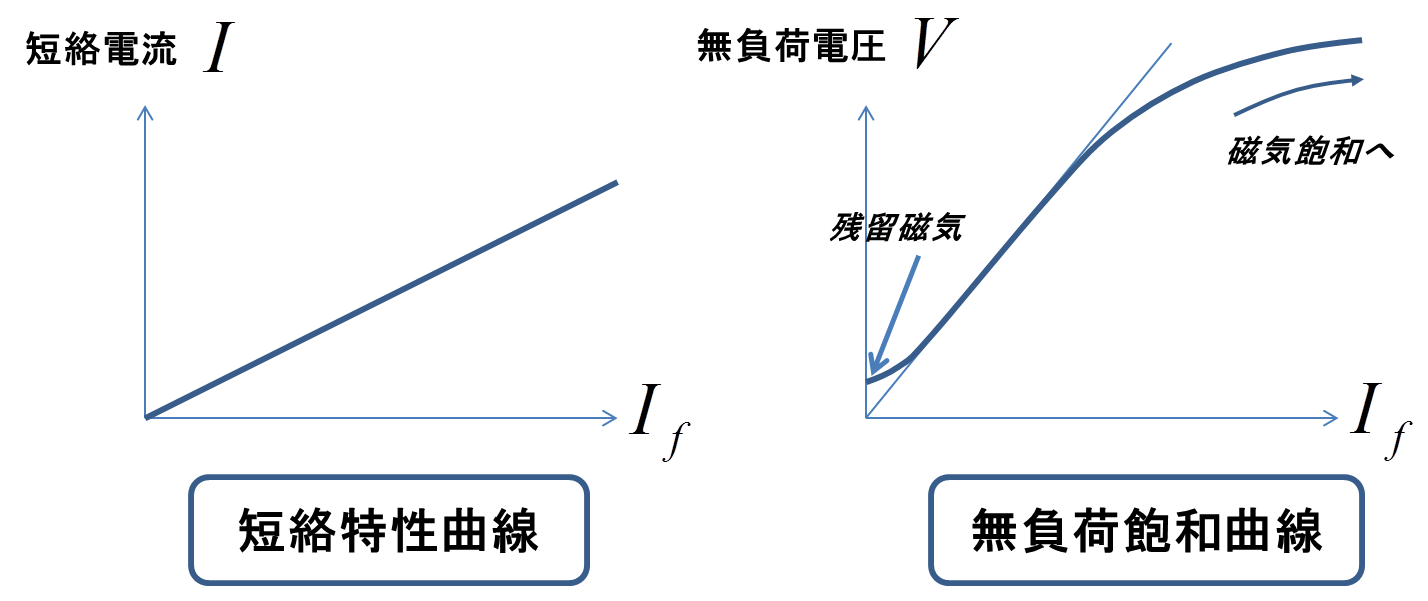
図4.短絡特性曲線（左）と無負荷飽和曲線（右）

 

　まず左側の短絡特性曲線はほぼ直線になる．それは図3の左側が実質的に変圧器となっていて，回転子コイルに流す励磁電流が，ある一定の変圧比で固定子コイルに流れて短絡電流として測定されるので，ある意味当然である．また右側の無負荷飽和曲線のこの形は鉄心の磁化曲線から説明ができる．

　この図4の２つのグラフは両方とも励磁電流\(I_{f}\)を横軸に取っているので下記の図5のように重ね書きできる．

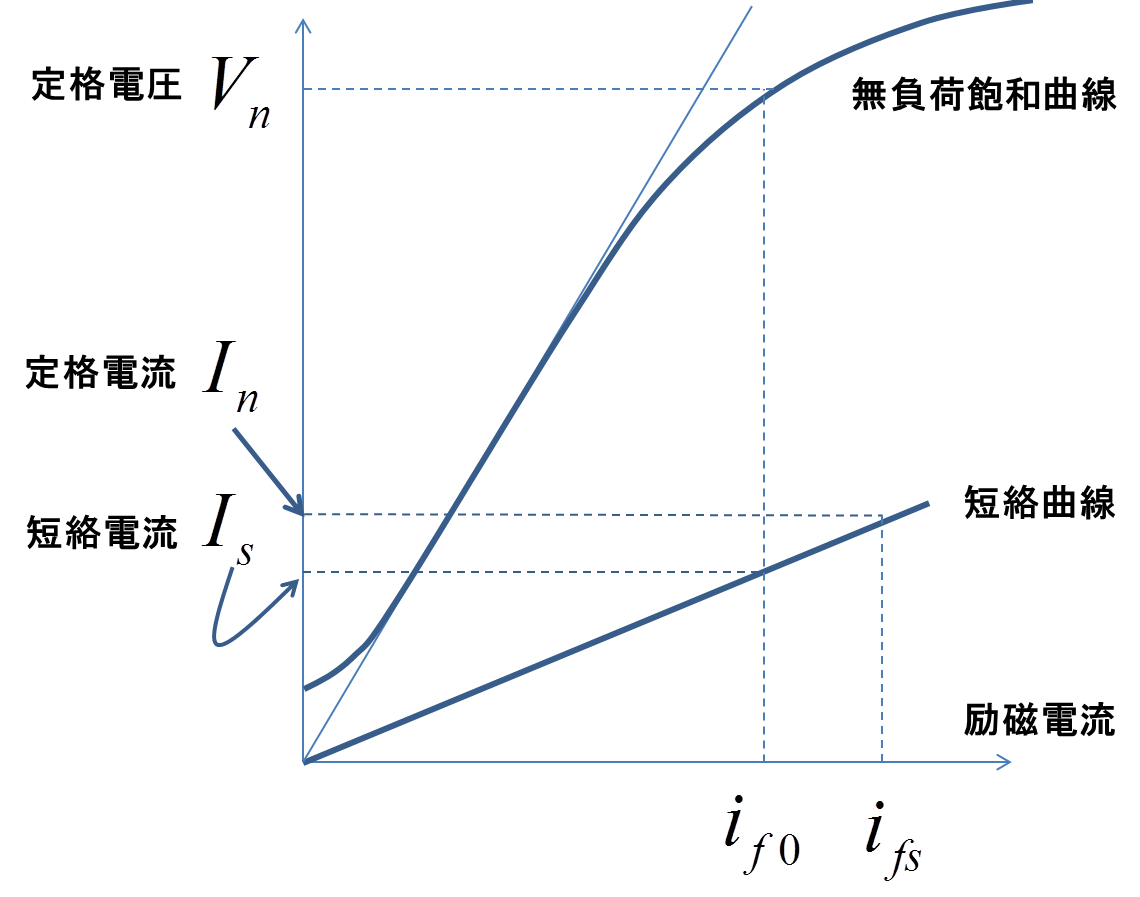
図5.短絡特性曲線と無負荷飽和曲線の重ね書き

 

　この図5のグラフ上で，短絡電流が定格電流\(I_{n}\)に等しくなる励磁電流\(i_{fs}\)と，無負荷端子電圧が定格電圧\(V_{n}\)に等しくなる励磁電流\(i_{f0}\)とをそれぞれ示している．この２つの励磁電流\(i_{fs}\)と\(i_{f0}\)との比が短絡比\(K_{s}\)に等しくなるのである．具体的には以下の通りである．

$$ K_{s}=\frac{i_{f0}}{i_{fs}} \tag{4} $$

　ここで，無負荷電圧を定格電圧\(V_{n}\)に等しくしたときの励磁電流\(I_{f0}\)における短絡電流を\(I_{s}\)だとして，短絡曲線が直線だとすると，図5から明らかに以下がいえる．

$$ I_{n}:I_{s}=i_{fs}:i_{f0} \tag{5} $$

すると，式（4）は次の式（6）のように書き換えることができる．

$$ K_{s}=\frac{I_{s}}{I_{n}} \tag{6} $$

短絡比は，短絡電流\(I_{s}\)と定格電流\(I_{n}\)の比であることがわかる．ただしこの短絡電流\(I_{s}\)は定格負荷運転のときの短絡電流ではなく，あくまで”無負荷時”に定格電圧にした状態からの短絡電流であることに注意する．

　最後に短絡比と電圧変動率が，定格運転時のベクトル図上でどのように表されるのかを考えてみよう．

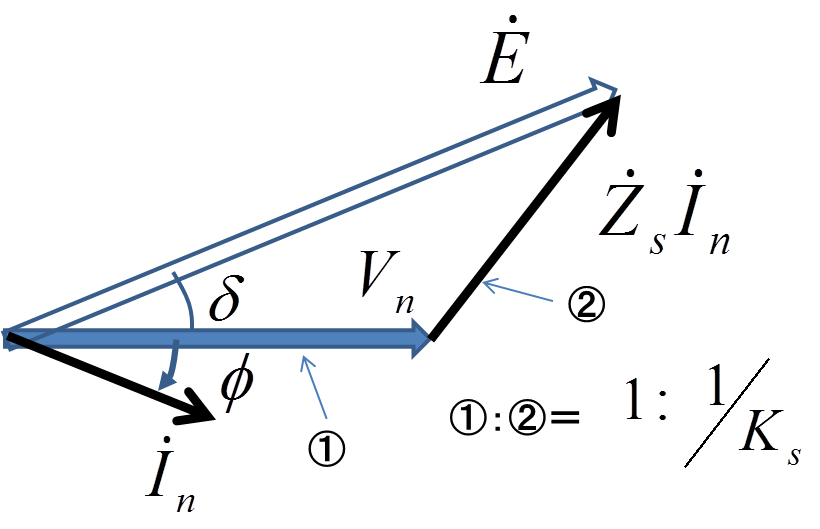
図6.短絡比と電圧変動率（力率角\(\phi\)）

 

　この図6は，定格力率角\(\phi\)で定格電流\(I_{n}\)，定格端子電圧\(V_{n}\)，同期インピーダンス\(Z_{s}\)としたときのベクトル図である．簡単に言うと端子電圧\(V_{n}\)を同期インピーダンス\(Z_{s}\)で割れば式（6）の短絡電流\(I_{s}\)になるので，

$$ V_{n}=Z_{s}I_{s} \tag{7} $$

と書ける．もちろん磁気飽和の効果を無視した上での関係式である．これを認めると式（6）から，

$$ K_{s}=\frac{I_{s}}{I_{n}}=\frac{Z_{s}I_{s}}{Z_{s}I_{n}}=\frac{V_{n}}{Z_{s}I_{n}} \tag{8} $$

と書き換えることができる．つまり，式（1）の定義に戻る．つまり，確かに式（4）の測定で短絡比を計算できているという証明ができた．ビジュアルで説明すると，短絡比というのは図6内の①と②の長さの比そのものである．

　続いて図6内で電圧変動率はどのように表されるかというと，端子電圧\(V_{n}\)の長さに対して起電力の大きさ\(E\)が何%増しなのかを見ればよい．以上で定格運転時のベクトル図上で２つの指標がどのように目算できるかわかったものと思う．

　最後に簡単に負荷特性曲線について触れておこう．図7をご覧いただきたい．

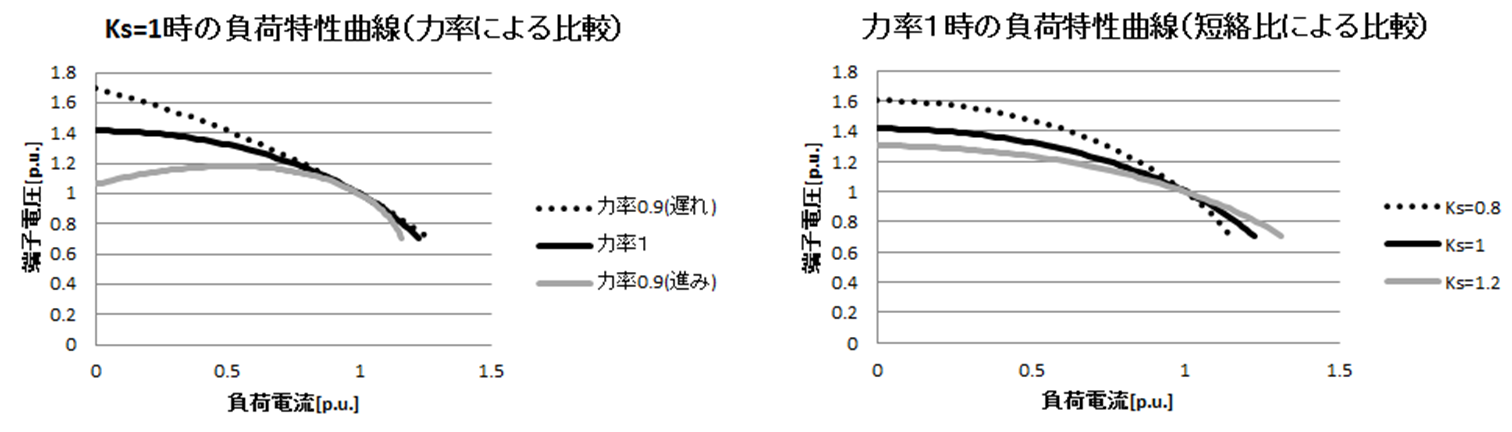
図7.負荷特性曲線

　図7に示すように，負荷特性曲線というのは，負荷電流を横軸に取ったときの端子電圧の推移を表しており，短絡比が大きいほうがフラットになっていることが見て取れる．電圧変動率が小さくなるので，端子電圧が負荷電流の多寡に依らなくなるのは自明である．この辺りの具体的な解析方法は著書をご覧いただきたい．

 

 

 

 

この項の内容に関する，より詳細で完全な解説は，

【徹底解説　電動機・発電機の理論】のP.175～P.184にて展開されています．是非ご参照を!!

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス